競技プログラミングの鉄則を読んでみて1

柴犬の4年前の写真です。9歳になったばかりのことで、きりっとした顔をしています。
概要
今読んでいる本は、著者 米田優峻氏の「競技プログラミングの鉄則 アルゴリズムと思考力を高める77の技術」です。
カラー刷りで図解も多く、解説も適切で私にとって理解が進む本です。応用問題も多く考えさせられます。
その中で、p143の応用問題「問題 B23」にちょっとてこずり、理解するのに2日程要しましたので自分の理解を記録することにします。
問題は巡回セールスマン問題と呼ばれるものでその内容は次の通りです。
二次元平面上にN(<=15)個の都市があり、それぞれ1からNまで番号が付けられています。
都市 i の座標は(Xi,Yi)です。
ある都から出発し、すべての都市を一度ずつ巡った後、出発した都市に戻ります。
この最短時間を求める。
解答
模範解答は次のようになっています。
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
int N, X[19], Y[19];
double dp[1 << 16][19];
int main() {
// 入力
cin >> N;
for (int i = 0; i < N; i++) cin >> X[i] >> Y[i];
// 配列 dp の初期化
for (int i = 0; i < (1 << N); i++) {
for (int j = 0; j < N; j++) dp[i][j] = 1e9;
}
// 動的計画法(dp[通った都市][今いる都市] となっている)
dp[0][0] = 0;
for (int i = 0; i < (1 << N); i++) {
for (int j = 0; j < N; j++) {
if (dp[i][j] >= 1e9) continue;
// 都市 j から都市 k に移動したい!
for (int k = 0; k < N; k++) {
// 既に都市 k を通っていた場合
if ((i / (1 << k)) % 2 == 1) continue;
// 状態遷移
double DIST = sqrt(1.0 * (X[j] - X[k]) * (X[j] - X[k]) + 1.0 * (Y[j] - Y[k]) * (Y[j] - Y[k]));
dp[i + (1 << k)][k] = min(dp[i + (1 << k)][k], dp[i][j] + DIST);
}
}
}
// 答えを出力
printf("%.12lf\n", dp[(1 << N) - 1][0]);
return 0;
}
分からなかったところ
分からないところ1
int i が i = 0 int j が j = 0 int k が k = 0 のとき dp[1][0] が作られるものの意味。
分からないところ2
dp[(1 << N) - 1][0] が答えになること。
理解したところ
分からないところ1
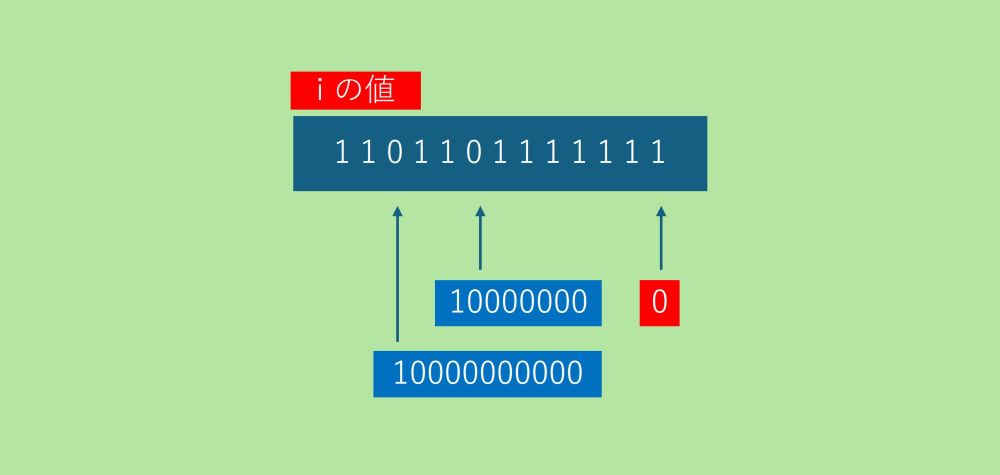
i の値が 1101101111111 の場合、次に選択できる都市の番号(k)は 10000000 か10000000000に限られます。
最終、都市の番号1は選択済み(i の一桁目が1のため)で決して戻ることはなく、都市の番号10000000か10000000000が最後の到達する都市です。
dp[1111111111111 ][10000000] か dp[1111111111111 ][10000000000] で終了します。
上のことに対して、i の値が 1101101111110 の場合、次に選択できる都市の番号は 0、10000000、10000000000に限られます。
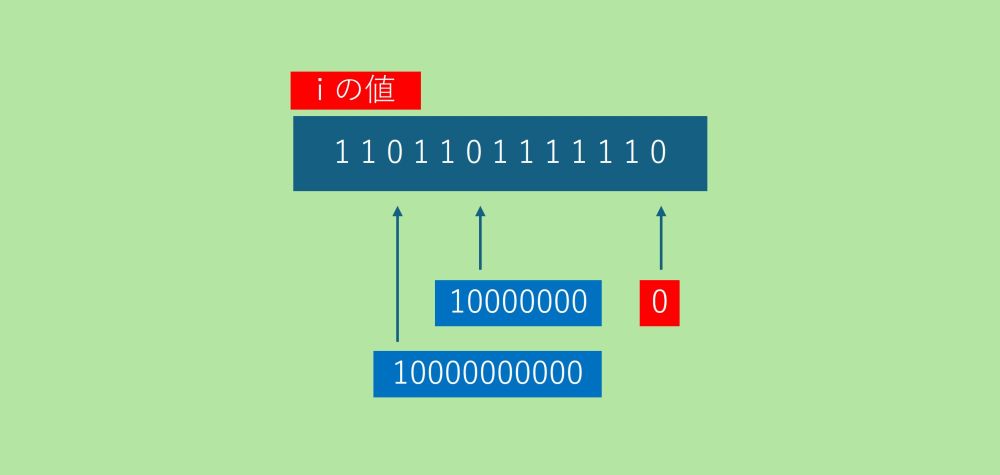
最後、都市の番号1(k=0)で終わるためには、都市の番号10000000か10000000000を通過した後都市の番号1 に行くことです。このとき i の値は 1111111111110 となります。
dp[1111111111110][10000000] か dp[1111111111110 ][10000000000] です。
都市の番号1(k=0)に来た時 i の値が 1111111111111( dp[1111111111111][0])となります。
分からないところ2
dp[(1 << N) – 1][0] が答えになることも理解できました。
解決したので、先に読み進めることにします。

