
このページでは掛け算「a × b 」を表す演算子を*とし、べき乗「a の b 乗」を表す演算子を ^ としています。
1の補数、2の補数
ある基準となる決まった数から別の数を引いた数を補数と呼んでいます。
10進法の場合
ある基準値を 1000 (10^3)として、別の数を123、375としてみます。
123 の補数は 1000 – 123 = 877
375 の補数は 1000 – 375 = 625
となります。これを 10 進法における 10 の補数(基数の補数)といいます。
次にある基準値を 999(10^3 – 1)として、同じ数値を使って求めてみます。
123 の補数は 999 – 123 = 876
375 の補数は 999 – 375 = 624
となります。これを 10 進法における 9 の補数(減基数の補数)といいます。
2進法の場合
ある基準値を 100000000 (2^8)として、別の数を01101100、10011111としてみます。
01101100 の補数は 100000000 – 01101100 = 10010100
10011111 の補数は 100000000 – 10011111 = 01100001
となります。これを 2 進法における 2 の補数(基数の補数)といいます。
ある基準値を 11111111 (2^8 – 1)として、別の数を01101100、10011111としてみます。
01101100 の補数は 11111111 – 01101100 = 10010011
10011111 の補数は 11111111 – 10011111 = 01100000
となります。これを 2 進法における 1 の補数(減基数の補数)といいます。
負の整数の表現に使用されるのは 2 進法における 2 の補数です。
負の整数
正の整数と負の整数の判別は、最上位ビットが 0 であれば正の整数、1 であれば負の整数という決め事があります。
たとえば、10000000 は -128 であり、01111111 は 127 という具合です。ここで「01111111 に 1 加えるだけで -128 なの?128 ではないの」という疑問が起こると思います。
最上位ビットが負を表していることを思い出してください。
10000000 は – (2^7) なので、
10000000 = 1*( – (2^7))+ 0*(2^6) + 0*(2^5)・・・+ 0*(2^1)+ 0*(2^0) は -128 となるのです。
下の表にまとめてみました。

8ビットであれば 0 から 255 までの数値を表すことできます。
0 から 127 まで(緑色部分)を正の数を表し、128 から 255 まで(オレンジ色部分)を負の整数で表すようにしているのです。
正の整数の負を求める簡単な方法
正の整数のビットを反転させて 1 を加えて求めることができます。
例えば 00101100 (10進法 44) であれば、反転させて 11010011 、これに 1 を加えて11010100 が 10 進法の -44 となります。
検証
下位7ビットの 1010100 は 1*64 + 0*32 +1*16 + 0*8 +1*4 + 0*2 + 0*1 = 84
最上位ビットの -128 を加えると -128 + 84 = -44 となり正しいことが分かります。
浮動点小数
単精度浮動小数点数では、符号部 1 ビット ・ 指数部 8 ビット ・ 仮数部 23 ビットで小数を表現します。
符号部は、 0 を正、1 を負とします。
仮数部は、整数部分が 1 であるような2進小数の小数部分を表し、先頭1を含めないドット以下表示になります。元の値の整数部分が 1001.・・・ なら右シフトして 1.001・・・ で仮数部は001・・・とします。0.000111・・・なら左シフトして 1.11・・・で仮数部 11・・・とします。
指数部は、単精度では中央値 127 でイクシス表現で表します。
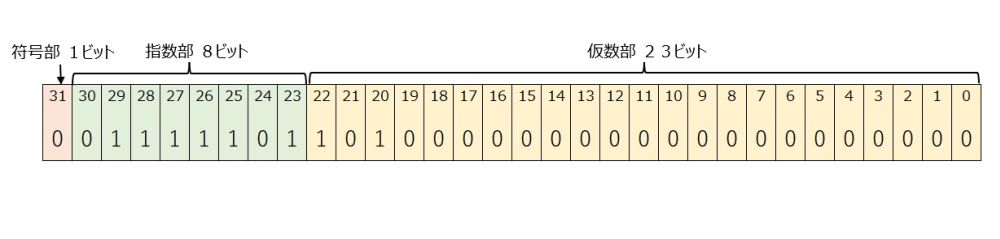
上の例ですと
符号部は、0ですから正の数値です。
指数部は 01111101 ですので、01111101 = 0 + 64 + 32 + 16 + 8 + 4 + 0 + 1 = 125
でイクシス表現に変換(中央値 127 を引きます。)すると 125 – 127 = -2 となり 2^(-2) をあらわしています。ただし、指数部おいてイクシス表現で扱う値は、規格により 1 から 254 までと決まっています。
2^(-2) = (1/2)*(1/2) = 1/4 = 0.25
となります。
仮数部は、ドット以下の部分ですので実際は 1.10100000000000000000000 を表しています。
1.10100・・・ = 1 + (2^(-1)) +0*(2^(-2)) + 1*(2^(-3)) + ・・・
= 1 + 0.5 +0.125 = 1.625
したがって、上の例ですと
0.25*1.625 = 0.40625 となります。
最大値
ここで演算に関する標準規格があり指数部の 1111111111 (10進法255)は無限大として使いますので、指数部の最大は 11111110 (10進法254)となります。
これまでのことから、最大値は 0_11111110_11111111111111111111111 と表せます。
1111111110 → 254 でイクセス表現だと 254 -127 = 127
11111111111111111111111 は 1.11111111111111111111111 であるから
1.11111111111111111111111 = 1 + 1 – 0.00000000000000000000001 = 2 – (2^(-23))
2^127 * (2 – (2^(-23)))
= 2^128 – 2^104
2^104乗は全体の100万分1以下なので無視し、(2^2) / 4 を掛けて
→ 2^128
= 2^130 / 4
= (2^10)^13 / 4
= ((1 +0.024)*10^3)^13 / 4
= ((1 + 0.024)^13)*10^39 / 4
(1 + 0.024)^13 を 1 + 13*0.024 に近似、10^39 / 4 は 2.5*(10^38)なので
→ (1 + 13*0.024)*2.5*(10^38)
= 3.280*(10^38) (概算ということでお許しください。正しくは、3.402e+38)
最小値
1_11111110_11111111111111111111111
符号部を 1 にするだけなので、最小値は -3.280*(10^38) となります。 (概算ということでお許しください。正しくは、-3.402e+38)
最小の正の数
表せる最小の正の数は、 0_00000000_00000000000000000000001 となりとなりそうですが、標準規格により指数部で表せる値 00000001 (10進法1)以上です。 00000000 (10進法0)はゼロに使います。
10進法にすると (2^(1 – 127))*(1 + 2^(-23)) となります。
(2^(1 – 127))*(1 + 2^(-23))
概算を求めますので 2^(-23) を無視します。
→ 2^(-126)
これに、16*(2^(-4)) を掛けます。
= (2^(-126)) *16*(2^(-4))
= 16*(2^(-130))
= 16 / (2^10)^13
= 16 / ((1 + 0.024)*10^3)^13
= 16 / ((1 + 0.024)^13*10^39)
(1 + 0.024)^13 を (1 + 13*0.024) に近似
→ (16 / ((1 + 13*0.024)*10^39)
= (16 / 1.312)*10^(-39)
= 12.19*10^(-39)
= 1.219*(10^(-38)) (概算ということでお許しください。正しくは、1.175e-38)
イクセス表現
0~255までの値を表すことができる場合,その中央の127を0とみなして,相対的に数値を差し引きした表現となります。0 を -127 と表し、255 が 128 を表すこととなる手法です。
ただし、IEEE Standard for Floating-Point Arithmetic (ANSI/IEEE Std 754-2008)により指数部の 0 と 255 は特別な意味をもちます。
倍精度浮動小数点数では、符号部 1 ビット ・ 指数部 11 ビット ・ 仮数部 52 ビットで小数を表現しますので、倍精度では 11111111111 /2 = 2047 / 2 = 1023 を中央値とします。
10進法から浮動点小数に変換
例えば10進法 65.625 を 2進法へ変換してみます。
65 > 1000001
0.625 > 1/2 + 1/(2^3) = 0.101
65.625 > 1000001.101
1000001.101 を先頭が 「1.・・・」となるまで、この場合は右シフト(0.00001・・なら左シフト)します。
1000001.101 = (2^6)*1.000001101 (6シフトしました。)
指数部は (2^6) となり 6 をイクセス表現すると127 + 6 = 133
133 を 2 進法にすると 10000101 となります。
従って、
10進法65.625 は 2進法0_10000101_00000110100000000000000で表現されます。